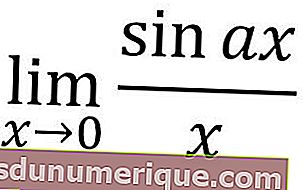Il limite della funzione trigonometrica è definito come il valore più vicino a un angolo nella funzione trigonometrica. Questo calcolo può essere sostituito come il limite di una funzione algebrica, ma con una funzione trigonometrica che deve essere prima modificata.
La funzione trigonometrica deve essere convertita in un'identità trigonometrica per un limite indefinito, che è un limite che se sostituito sarà 0. Inoltre, c'è anche un modo per calcolare un limite indefinito senza utilizzare un'identità trigonometrica, ma utilizzando il teorema del limite trigonometrico. Altri usano simultaneamente identità e teorema.
Per determinare il valore limite delle funzioni trigonometriche, ci sono vari modi che possono essere usati, vale a dire metodi numerici, sostituzione, factoring, peer time e derivati.
(Leggi anche: Misurare la visibilità utilizzando formule trigonometriche)
Ma in base al valore, possiamo dividere questa formula in due, cioè quelli che sono vicini al numero e vicini allo zero.
X Avvicinamento a un numero
Se abbiamo il limite della funzione trigonometrica la cui x si avvicina al numero c, possiamo determinarne il valore sostituendo c nella funzione trigonometrica. Le formule sono le seguenti.

X in avvicinamento allo zero
Se la x del limite di una funzione trigonometrica si avvicina a zero, possiamo usare le formule seguenti.

Se dopo aver sostituito il valore x nella funzione trigonometrica la forma indefinita è 0/0 ∞ / ∞, allora per determinare il valore limite della funzione trigonometrica, puoi usare la regola di L'Hospital, vale a dire
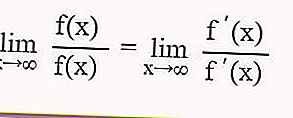
Intuizione Comprensione dei limiti della funzione trigonometrica
Comprendere intuitivamente il limite di una funzione trigonometrica è lo stesso del limite di una funzione algebrica. Il limite della funzione trigonometrica esiste se e solo se esistono il limite sinistro e il limite destro e il limite sinistro è uguale al limite destro.