Fai attenzione, se il tetto della casa e la tenda hanno quasi la stessa forma? Se guardi di nuovo, sembra che sia composto da 2 triangoli a ciascuna estremità, quindi coperto da una coperta rettangolare. Questa forma è anche nota come prisma triangolare. Si chiama così perché la base e il coperchio sono triangolari. In geometria, studieremo la definizione e la formula dei prismi triangolari. In questa occasione discuteremo anche vari esempi del problema per poter comprendere meglio questo materiale.
Un prisma è una forma che ha un coperchio e una base con una forma n-lati congruente, mentre i lati verticali sono rettangolari.
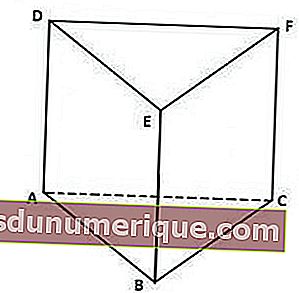
I prismi triangolari hanno le seguenti caratteristiche:
Presenta base e coperchio triangolari congruenti.
Dall'immagine sopra, il coperchio del prisma, ovvero il triangolo DEF, ha la stessa forma e dimensione del triangolo ABC come base.
Rettangolo come lato verticale.
Puoi vedere, il prisma sopra è limitato da tre rettangoli su ciascun lato della verticale, vale a dire i rettangoli ACFD, BCFE e ABED.
Ha 5 lati, 9 bordi e 6 vertici.
I 5 lati di un prisma triangolare sono costituiti da 1 lato della base, 1 lato del coperchio e 3 lati della verticale. Mentre le 9 costole sono costituite da 3 costole verticali, 3 lati della base e 3 del lato del coperchio. Inoltre, i 6 vertici sono i punti A, B, C, D, E e F.
Ora che conosciamo le caratteristiche e anche il significato di un prisma triangolare, è tempo per noi di conoscere le formule del prisma triangolare e gli esempi dei loro problemi.
Formule del prisma triangolare e problemi di esempio
Ci saranno 2 tipi di formule del prisma triangolare che impareremo. La formula per trovare il volume e la formula per trovare l'area della superficie. Le formule sono così:
Volume
Per il volume, useremo la formula:
V = area della base × altezza
o
V = (½ x a x h) × altezza del prisma
Quindi, per capirlo meglio, diamo un'occhiata a un esempio di questo problema:
Un prisma è alto 10 cm. La base del prisma ha la forma di un triangolo rettangolo con lunghezze laterali di 4 cm e 3 cm, rispettivamente. Qual è il volume di questo prisma triangolare?
Soluzione:
Qui, dobbiamo solo inserire i numeri noti in una formula come questa:
V = (½ x a x h) × altezza del prisma
V = (½ x 4 x 3) × 10
V = 6 × 10
V = 60 cm 3
Superficie
Nel calcolare l'area della superficie di un prisma triangolare, useremo una formula come questa:
L = (2 x area della base) + (area di tutti i lati perpendicolari)
se il triangolo è equilatero, puoi usare la formula:
L = (2 x area della base) + (3 x area di un lato della verticale)
Oppure potrebbe essere la formula:
L = (2 x area della base) + (perimetro della base x altezza del prisma)
Diamo un'occhiata a un esempio di questo problema per vedere come viene applicata questa formula. Ecco un esempio del problema:
C'è un prisma triangolare equilatero che ha un'altezza di 12 cm, una lunghezza laterale di 5 cm e un'altezza di 8 cm. Allora qual è la superficie di questo prisma triangolare?
Soluzione:
Per trovare l'area della superficie, usiamo semplicemente la formula per l'area della superficie di un prisma triangolare come questo:
L = (2 x area della base) + (3 x area di un piano verticale)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 cm 2
Quindi queste sono le varie formule del prisma triangolare che dovresti conoscere, così come alcuni esempi di problemi. Se sei ancora confuso, puoi chiedere nella colonna dei commenti, oppure puoi provare Smart Class, la piattaforma di tutoraggio online affidabile in World.