Solo così sai, le relazioni esistono anche in matematica, sai. Esistono relazioni nel materiale relativo ai set. Le relazioni sono regole che collegano i membri di un insieme con altri membri dell'insieme. La relazione dall'insieme A all'insieme B collega i membri dell'insieme A ai membri dell'insieme B. In questa opportunità impareremo esempi di relazioni e le loro proprietà, oltre a vari esempi di problemi che possono aiutarti a comprendere meglio questo materiale.
Esempi di relazioni e loro natura
La relazione può essere definita come una regola che collega membri dell'area di origine (dominio) e membri di un'area amica (codominio). In una relazione, non ci sono regole speciali che devono essere soddisfatte per abbinare i membri dell'associazione regionale ai membri delle regioni amiche.
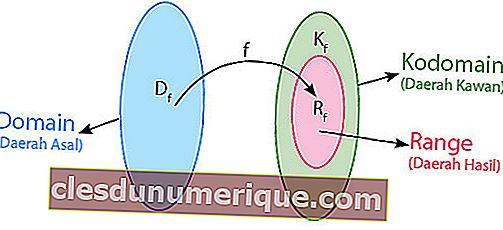
fonte: idschool.net
Ogni membro dell'associazione regionale di origine può avere più di un partner o non può avere un partner affatto. La relazione di due insiemi può essere espressa in tre modi, vale a dire:
- Diagramma a freccia
- Diagramma cartesiano.
- L'insieme di coppie consecutive
Quanto segue è un'ulteriore spiegazione dei tre modi:
Grafici a freccia
I grafici a freccia sono il modo più semplice per esprimere una relazione. Questo diagramma formerà un modello di una relazione sotto forma di una freccia che mostra la relazione dai membri dell'insieme A ai membri dell'insieme B.
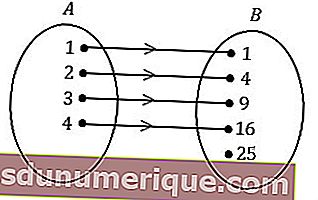
Fonte: maretong.com
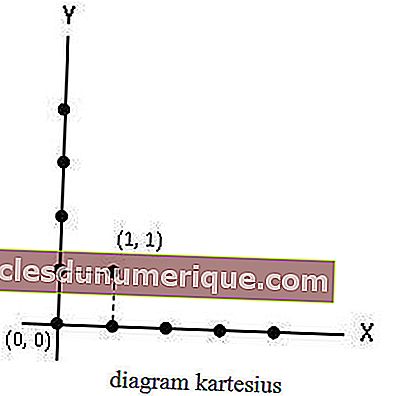
Diagramma cartesiano
Il diagramma cartesiano è un diagramma costituito da un asse X e un asse Y. In un diagramma cartesiano, gli elementi dell'insieme A si trovano sull'asse X, mentre gli elementi dell'insieme B si trovano sull'asse Y. Le relazioni che collegano l'insieme A a B sono indicate da punti o punti.
Set di coppie sequenziali
Una relazione che collega un insieme a un altro può essere rappresentata sotto forma di un insieme di coppie ordinate. Il modo di scrivere è che i membri dell'insieme A vengono scritti per primi, mentre i membri dell'insieme B che sono le coppie vengono scritti per secondi.
Esempi come questo:
A = Set mondiale, Giappone, Corea, Francia
Set B = Tokyo, Parigi, Giacarta, Seoul
Determina l'insieme ordinato di coppie per paese e capitale.
Risposta:
{(World, Jakarta), (Japan, Tokyo), (Korea, Seoul), (France, Paris)}
Funzione
Una funzione o mappatura è una relazione speciale dall'insieme A all'insieme B, con la regola che ogni membro dell'insieme A è accoppiato esattamente uno al membro dell'insieme B.
Il risultato della mappatura da dominio a dominio è chiamato intervallo di funzioni o area dei risultati. Analogamente alle relazioni, le funzioni possono essere rappresentate anche sotto forma di diagrammi a freccia, coppie ordinate e diagrammi cartesiani.
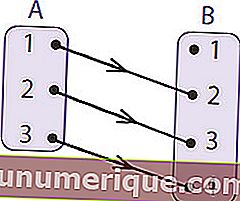
Fonte: rumushitung.com
Per capirlo ulteriormente, considera l'immagine sopra. L'insieme A o l'area di origine è chiamato dominio. L'insieme B che è un'area amico è chiamato codominio. Il membro dell'area amichevole che è il risultato della mappatura è chiamato area di resa o gamma di funzioni. Quindi dal diagramma a freccia sopra si può concludere che
- Il dominio (D f) è A = {1,2,3}
- Codomain è B = {1,2,3,4}
- Intervallo / Risultato (R f) è = {2,3,4}
Le funzioni possono essere indicate con lettere minuscole come f, g, h, i e così via. La funzione f mappa l'insieme A per l'insieme B, quindi può essere indicata con f (x): A → B.
Un esempio è la funzione f che mappa A su B con la regola f: x → 2x + 2. Dalla notazione della funzione, x è un membro del dominio. La funzione x → 2x + 2 significa che la funzione f mappa x su 2x + 2. Quindi l'area di x dalla funzione f è 2x + 2. Quindi puoi denotarla come f (x) = 2x +2.
Se la funzione f: x → ax + b con x è un membro del dominio f, la formula per la funzione f è
f (x) = ax + b
Esempio di problemi:
Data la funzione f: x → 2x - 2 dove x è un numero intero. Prova a determinare il valore di f (3).
Soluzione:
La funzione f: x → 2x - 2 può essere rappresentata da f (x) = 2x - 2
così,
f (x) = 2x - 2
f (3) = 2 (3) - 2 = 4
Quindi questo è un esempio di relazioni e funzioni in matematica. Hai domande in merito? Scrivi la tua domanda nella colonna dei commenti e non dimenticare di condividere questa conoscenza.