In matematica, uno schema numerico è una disposizione di diversi numeri che formano un certo schema. Diversi tipi di modelli numerici includono modelli pari, dispari, aritmetici e geometrici. Oggi parleremo di due tipi di modelli numerici, vale a dire linea geometrica e serie geometrica.
Una linea geometrica è una sequenza di numeri composta da termini che hanno proporzioni fisse. Il primo termine della sequenza geometrica è denotato da a. Il rapporto o confronto tra due termini è indicato con r.
Le linee di geometria possono essere formulate come segue.
a, ar, ar2, ar3,…, arn-
a = il primo termine della sequenza geometrica
r = il rapporto tra i termini
n = sequenza di termini
Per determinare il valore dell'ennesimo termine o rapporto, possiamo usare la seguente formula.
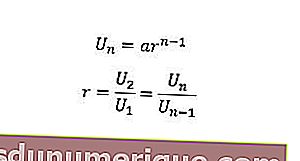
U n = l'ennesimo termine
Lavoriamo su un problema di esempio di seguito.
Data una sequenza geometrica 3, 9, 27, 81, 243. Sulla base di questo, quindi determinare il rapporto della sequenza geometrica!
Sappiamo U 1 = 3 e U 2 = 9, quindi se li inseriamo nella formula, otterremo il seguente risultato.
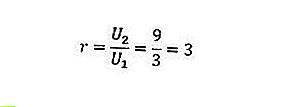
Quindi, il rapporto o il confronto della sequenza geometrica sopra è 3.
(Leggi anche: Logica matematica, dalla negazione alla biimplicazione)
Nel frattempo, una serie geometrica è la somma dei termini in una sequenza geometrica. Una serie geometrica può essere indicata con S n che significa il numero dei primi n termini nella sequenza geometrica.
La serie geometrica può essere formulata come segue.

a = il primo termine della sequenza geometrica
r = il rapporto tra i termini
n = sequenza dell'ultimo termine aggiunto
U n = l'ennesimo termine
Lavoriamo su un problema di esempio di seguito.
Dato che una serie geometrica con il primo termine è 6 e il quarto termine è 48, allora la somma dei primi sei termini è ...?
Sappiamo che a = 6 e U 4 = 48. Se inseriamo la formula, il risultato sarà il seguente.
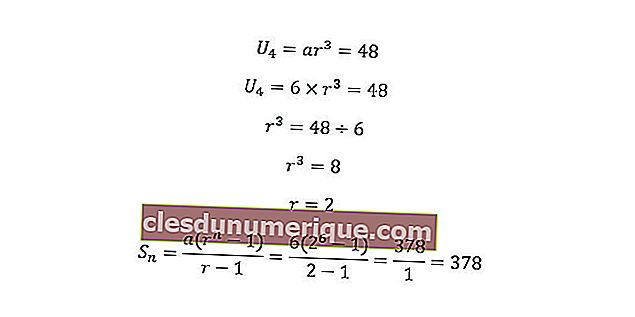
Quindi, la somma dei primi 6 termini della serie precedente è 378.